注意：二重积分要满足面积微元 $d\sigma>0$

概念

• 和式极限：($D$ 不是一般的平面有界闭区域，而是一个长方形区域 $[a,b]\times[c,d]$)

• 普通对称性：

  • 若 $D$ 关于 $y$ 轴对称，则

    $D_1$ 是 $D$ 在 $y$ 轴左或右侧的部分。

  • 若 $D$ 关于 $x$ 轴对称，则

    $D_1$ 是 $D$ 在 $x$ 轴上或下侧的部分。

  • 若 $D$ 关于原点对称，则

    $D_1$ 是 $D$ 关于原点对称的半个部分。

  • 若 $D$ 关于 $y=x$ 对称，则

    $D_1$ 是 $D$ 关于 $y=x$ 对称的半个部分。

  • 若 $D$ 关于 $y=a$ 对称，则

    $D_1$ 是 $D$ 在 $y=a$ 上或下侧的部分。

  • 若 $D$ 关于 $x=a$ 对称，则

    $D_1$ 是 $D$ 在 $x=a$ 左或右侧的部分。

• 轮换对称性：若将 $D$ 中的 $x,y$ 对调后，$D$ 不变 (即 $D$ 关于 $y=x$ 对称)，则有

  若 $f(x,y)+f(y,x)=(>)a$，则

  轮换对称性是积分值与字母无关理论下的一种特殊情形。

• 二重积分比大小：

  • 用对称性
  • 用保号性

• 周期性：若化为累次积分后，一元积分有用周期性的机会，则可化简计算。

• 二重积分中值定理：存在 $(\xi,\eta)\in D$ ，使得 $\iint\limits_Df(x,y)d\sigma=f(\xi,\eta)\cdot S$ 成立，$S$ 是区域 $D$ 的面积。

计算

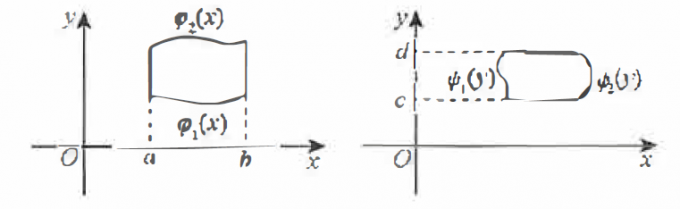
• 直角坐标系与换序：在直角坐标系下，按照积分次序的不同，一般将二重积分的计算分为两种情况：(后积先定限，限内画条线，先交写下限，后交写上限)

  • $\large\iint\limits_D f(x,y)d\sigma=\int_a^bdx\int_{\varphi_1(x)}^{\varphi_2(x)}f(x,y)dy$，其中 $D$ 为 $X$ 型区域：$\varphi_1(x)\leq y\leq\varphi_2(x),a\leq x\leq b$；
  • $\large\iint\limits_D f(x,y)d\sigma=\int_c^ddy\int_{\psi_1(y)}^{\psi_2(y)}f(x,y)dx$，其中 $D$ 为 $Y$ 型区域：$\psi_1(y)\leq x\leq\psi_2(y),c\leq y\leq d$。

  

• 极坐标系与换序：在极坐标系下，按照积分区域与极点位置关系的不同，一般将二重积分的计算分为三种情况：

  • 极点 $O$ 在区域 $D$ 外部：$\large\iint\limits_D f(x,y)d\sigma=\int_\alpha^\beta d\theta\int_{r_1(\theta)}^{r_2(\theta)}f(r\cos\theta,r\sin\theta)rdr$；
  • 极点 $O$ 在区域 $D$ 边界上：$\large\iint\limits_D f(x,y)d\sigma=\int_\alpha^\beta d\theta\int_{0}^{r(\theta)}f(r\cos\theta,r\sin\theta)rdr$；
  • 极点 $O$ 在区域 $D$ 内部：$\large\iint\limits_D f(x,y)d\sigma=\int_0^{2\pi} d\theta\int_{0}^{r(\theta)}f(r\cos\theta,r\sin\theta)rdr$。

• 直极互化：

  • 关于积分区域 $D$：

    • 图形变换：

      • 平移变换：

        • 将函数 $y=f(x)$ 的图像沿 $x$ 轴向左平移 $x_0(x_0>0)$ 个单位长度，得到函数 $y=f(x+x_0)$ 的图像；将函数 $y=f(x)$ 的图像沿 $x$ 轴向右平移 $x_0(x_0>0)$ 个单位长度，得到函数 $y=f(x-x_0)$ 的图像。(左加右减)
        • 将函数 $y=f(x)$ 的图像沿 $y$ 轴向上平移 $y_0(y_0>0)$ 个单位长度，得到函数 $y=f(x)+y_0$ 的图像；将函数 $y=f(x)$ 的图像沿 $y$ 轴向下平移 $y_0(y_0>0)$ 个单位长度，得到函数 $y=f(x)-y_0$ 的图像。(上加下减)

      • 对称变换：

        • 将函数 $y=f(x)$ 的图像关于 $x$ 轴对称，得到函数 $y=-f(x)$ 的图像；
        • 将函数 $y=f(x)$ 的图像关于 $y$ 轴对称，得到函数 $y=f(-x)$ 的图像；
        • 将函数 $y=f(x)$ 的图像关于原点对称，得到函数 $y=-f(-x)$ 的图像；
        • 将函数 $y=f(x)$ 的图像关于直线 $y=x$ 对称，得到函数 $y=f^{-1}(x)$ 的图像；
        • 保留函数 $y=f(x)$ 在 $x$ 轴及 $x$ 轴上方的部分，把 $x$ 轴下方的部分关于 $x$ 轴对称到 $x$ 轴上方并去掉原来下方的部分，得到函数 $y=|f(x)|$ 的图像；
        • 保留函数 $y=f(x)$ 在 $y$ 轴及 $y$ 轴右侧的部分，去掉 $y$ 轴左侧的部分，再将 $y$ 轴右侧图像对称到 $y$ 轴左侧，得到函数 $y=f(|x|)$ 的图像；

      • 伸缩变换：

        • 水平伸缩：$y=f(kx)(k>1)$ 的图像，可由 $y=f(x)$ 的图像上每点的横坐标缩短到原来的 $\frac{1}{k}$ 倍且纵坐标不变得到；$y=f(kx)(0<k<1)$ 的图像，可由 $y=f(x)$ 的图像上每点的横坐标伸长到原来的 ${\frac{1}{k}}$ 倍且纵坐标不变得到。
        • 垂直伸缩：$y=kf(x)(k>1)$ 的图像，可由 $y=f(x)$ 的图像上每点的纵坐标伸长到原来的 ${k}$ 倍且横坐标不变得到；$y=kf(x)(0<k<1)$ 的图像，可由 $y=f(x)$ 的图像上每点的纵坐标缩短到原来的 $\frac{1}{k}$ 倍且横坐标不变得到。

    • 直角系方程给出：

      • 已知曲线：可直接画出
      • 未知曲线：描特殊点 (有时可定出定义域、值域)；用图形变换；用导数工具 (一阶导数定单调、驻点；二阶导数定凹凸、拐点等)

    • 极坐标方程给出：

      • 已知曲线：可直接画出
      • 未知曲线：描特殊点；用图形变换；极直互化

    • 参数方程给出：

      • 已知曲线：可直接画出
      • 未知曲线：描点法；化为极、直方程

    • 动区域 (含其他参数)

  • 关于被积函数 $f(x,y)$：

    • 分段函数（含绝对值）
    • 最大、最小值函数
    • 取整函数
    • 符号函数 $sgn(u)=\begin{cases}1,u>0\\0,u=0\\-1,u<0\end{cases}$
    • 抽象函数
    • 复合函数
    • 偏导函数

  • 换元法：二重积分亦有如定积分一脉相承的换元法，有时很有用，若能够用上，可直接使用，不必证明：

应用

• 面积：

下面四个考点均为数学一。

• 曲顶柱体体积：曲顶为 $z=z(x,y),(x,y)\in D_{xy}$ 的柱体体积

• 总质量：

• 重心坐标：

• 转动惯量：对于平面薄片，面密度为 $\rho(x,y)$，$D$ 是薄片所占的平面区域，则计算该薄片对 $x$ 轴、$y$ 轴和原点 $O$ 的转动惯量 $I_x,I_y,I_O$ 公式分别为

  $$

  $$